80 High Correlation Filter

80.1 High Correlation Filter

We are looking to remove correlated features. By correlated features, we typically talk about Pearson correlation. The methods in this chapter don’t require that Pearson correlation is used, just that any correlation method is used. Next, we will look at how we can remove the offending variables. We will show an iterative approach and a clustering approach. Both methods are learned methods as they identify variables to be kept.

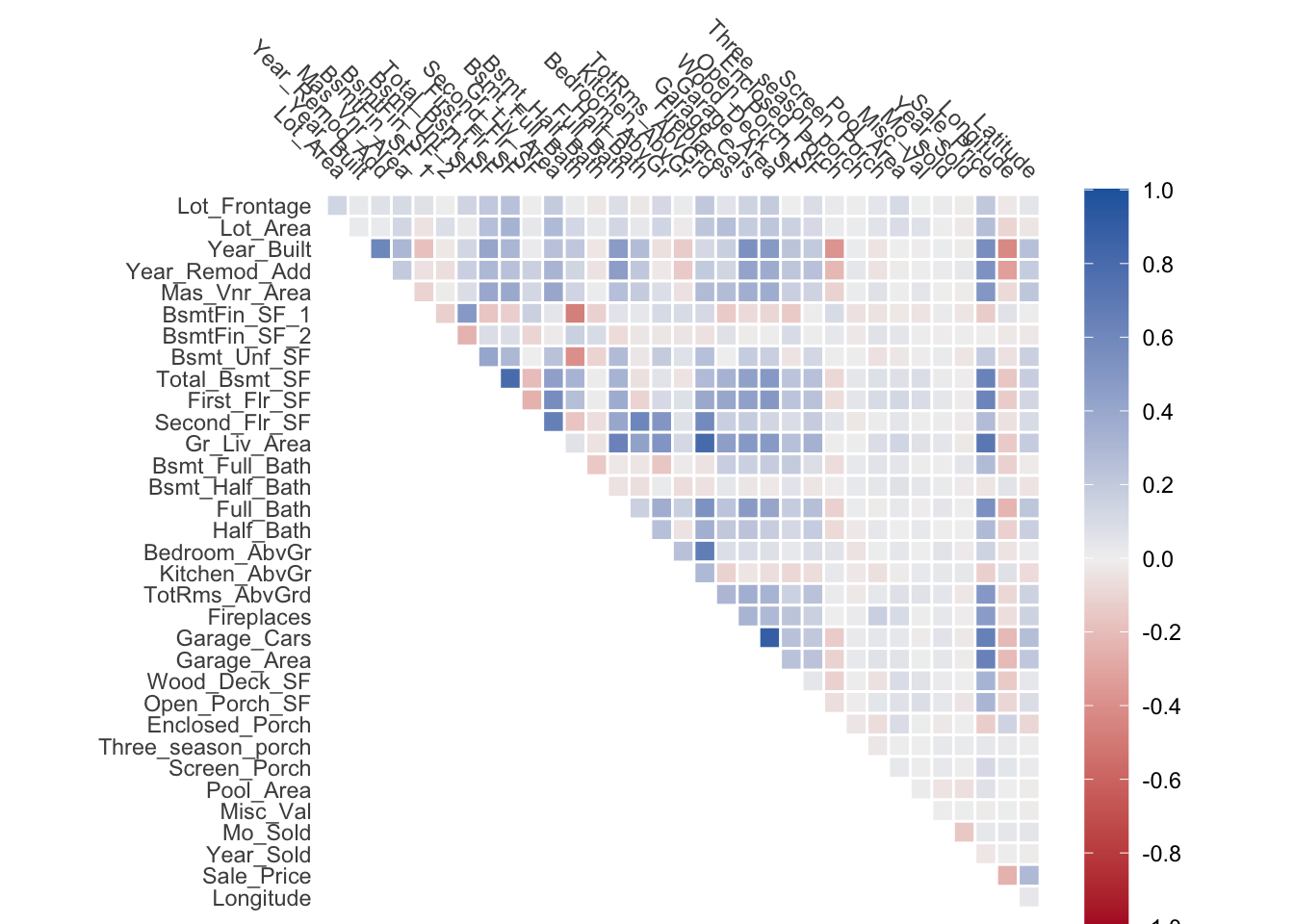
I always find it useful to look at a correlation matrix first

Correlation chart. — Figure 80.1: Some clusters of correlated features.

looking at the above chart we see some correlated features. One way to perform our filtering is to find all the correlated pairs over a certain threshold and remove one of them. Below is a chart of the 10 most correlated pairs

Table 80.1: Some predictors appear multiple times in this table.

x	y	r
Garage_Cars	Garage_Area	0.890
Gr_Liv_Area	TotRms_AbvGrd	0.808
Total_Bsmt_SF	First_Flr_SF	0.800
Gr_Liv_Area	Sale_Price	0.707
Bedroom_AbvGr	TotRms_AbvGrd	0.673
Second_Flr_SF	Gr_Liv_Area	0.655
Garage_Cars	Sale_Price	0.648
Garage_Area	Sale_Price	0.640
Total_Bsmt_SF	Sale_Price	0.633
Gr_Liv_Area	Full_Bath	0.630

One way to do filtering is to pink a threshold and repeatably remove one of the variables of the most correlated pair until there are no pairs left with a correlation over the threshold. This method has a minimal computational footprint as it just needs to calculate the correlations once at the beginning. The threshold is likely to need to be tuned as we can’t say for sure what a good threshold is. With the removal of variables, there is always a chance that we are removing signal rather than noise, this is increasingly true as we remove more and more predictors.

TODO

rewrite this as an algorithm

If we look at the above table, we notice that some of the variables occur together. One such example is Garage_Cars, Garage_Area and Sale_Price. These 3 variables are highly co-correlated and it would be neat if we could deal with these variables at the same time.

TODO

find a different example so Sale_Price isn’t part of this as it is usually the outcome.

TODO

Add a good graph showing this effect.

What we could do, is take the correlation matrix and apply a clustering model on it. Then we use the clustering model to lump together the groups of highly correlated predictors. Then within each cluster, one predictor is chosen to be kept. The clusters should ideally be chosen such that uncorrelated predictors are alone in their cluster. This method can work better with the global structure of the data but requires fitting and tuning another model.

80.2 Pros and Cons

80.2.1 Pros

Computationally simple and fast
Easily explainable. “Predictors were removed”
Will lead to a faster and simpler model

80.2.2 Cons

Can be hard to justify. “Why was this predictor kept instead of this one?”
Will lead to loss of signal and performance, with the hope that this loss is kept minimal

80.3 R Examples

We will use the ames data set from {modeldata} in this example. The {recipes} step step_corrr() performs the simple correlation filter described at the beginning of this chapter.

library(recipes)
library(modeldata)

corr_rec <- recipe(Sale_Price ~ ., data = ames) |>
  step_corr(all_numeric_predictors(), threshold = 0.75) |>
  prep()

We can see the variables that were removed with the tidy() method

corr_rec |>
  tidy(1)

# A tibble: 3 × 2
  terms        id        
  <chr>        <chr>     
1 First_Flr_SF corr_Bp5vK
2 Gr_Liv_Area  corr_Bp5vK
3 Garage_Cars  corr_Bp5vK

We can see that when we lower this threshold to the extreme, more predictors are removed.

recipe(Sale_Price ~ ., data = ames) |>
  step_corr(all_numeric_predictors(), threshold = 0.25) |>
  prep() |>
  tidy(1)

# A tibble: 13 × 2
   terms          id        
   <chr>          <chr>     
 1 Bsmt_Unf_SF    corr_RUieL
 2 Total_Bsmt_SF  corr_RUieL
 3 First_Flr_SF   corr_RUieL
 4 Gr_Liv_Area    corr_RUieL
 5 Bsmt_Full_Bath corr_RUieL
 6 Full_Bath      corr_RUieL
 7 TotRms_AbvGrd  corr_RUieL
 8 Fireplaces     corr_RUieL
 9 Garage_Cars    corr_RUieL
10 Garage_Area    corr_RUieL
11 Year_Built     corr_RUieL
12 Second_Flr_SF  corr_RUieL
13 Year_Remod_Add corr_RUieL

80.4 Python Examples

I’m not aware of a good way to do this in a scikit-learn way. Please file an issue on github if you know of a good way.